概率论前两章复习
brief
本博文收集《概率论与数理统计 第五版 习题全解指南(浙大 第5版) (盛骤、谢式千、潘承毅)》前两章随机事件与概率和随机变量及其概率分布的基础概念,典型例题及求解。
例题索引
课时1
P25: 2, 3, 4,
P 26: 8, 12
课时2
P 26: 14,
P27: 22, 23,26, 28, 29
P28:34
P29:36,37
课时3
P56: 2, 4, 6, 9
P57: 12, 15,16, 18
课时4
P58: 20,23,
P59: 24, 25,29, 30,
P60: 34,36
1.随机事件与概率
常见符号
E随机试验Ω样本空间F子集组成的集合ω样本点
1.1随机事件
随机事件简称事件
基本运算和运算规律
事件的并——>和事件
事件的交——>积事件
事件的差 A−B⇔w∈A但w∈/B⇔A发生但B不发生
不相容 AB=∅
交换律,结合律(相同符号),分配律(不同符号,理解成互相做加号和乘号)
德摩根律
不相容分解 A∪B=A∪AˉB,A=AB∪ABˉ
例题

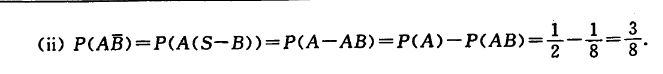
注意这种换算方法就行
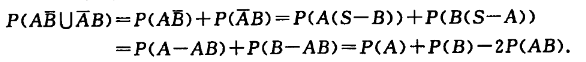
事件域和事件的关系

有限样本空间和可列无穷样本空间的每个子集均为事件。
1.2 频率和概率
频率
非负性,规范性,可列可加性


概率
定义 设 E是随机试验,S 是它的样本空间对于 E的每一事件 A 赋予一个实数,记为 P(A),称为事件 A 的概率如果集合函数 P(·)满足下列条件

另外有不可能事件的概率为0
有限可加
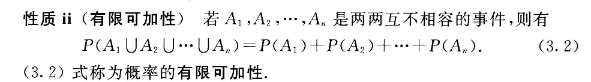
可减性

逆事件的概率 P(Aˉ)=1−P(A)
加法公式

1.3古典概型
古典概型
- 试验中只有有限个可能的结果
- 试验的每个基本事件发生的可能性相同
P(A)=Ω中元素的个数A中元素个数=nA中元素个数
有限等可能概型(Ω,F,P)
如随机试验,将一枚硬币指头三次,恰好几次正面的情况
注意这里A中元素个数的定义

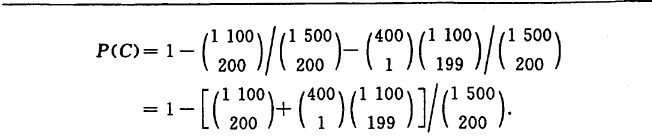
几何概型
两个特征
- 试验所有可能的结果形成Rn的一个有界区域Ω
- 对子集A ⊂ $\Omega $,试验的结果落入A的概率与A的测读S(A)而和A的位置和形状无关
P(A)=S(Ω)S(A)
1.4 条件概率
如文两个小孩一男一女的概率,现在已知至少有一位女孩
P(A∣B)已知事件B发生条件下,事件A发生的概率
P(A∣B)=P(B)P(AB)

additionally
P(B∣B)=1,P(Bˉ∣B)=0P(A)=P(A∣Ω)

乘法公式
P(AB)=P(B)P(A∣B)P(ABC)=P(C∣AB)P(B∣A)P(A)P(A1A2...An)=P(A1)P(A2∣A1)P(A3∣A1A2)⋯P(An∣A1⋯An−1)
全概率公式
完备事件组

B1,B2⋯Bn为完备事件组
设(Ω,F,P)为概率空间,B1,B2⋯Bn为完整事件组,则对任何事件A∈F,
P(A)=t=1∑nP(Bi)P(A∣Bi)若B1…Bn…为完备事件组P(A)=t=1∑∞P(Bi)P(A∣Bi)
理解:已知各个事件产生结果事件的概率,求结果事件发生的总概率
更常用的有
P(A)=P(B)P(A∣B)+P(Bˉ)P(A∣Bˉ)
贝叶斯公式
P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi),i=1,⋯,n同时若B1...Bn...为完备事件组,P(A)>0则P(Bi∣A)=∑j=1∞P(Bj)P(A∣Bj)P(Bi)P(A∣Bi),i=1,⋯,n,⋯
理解:已知结果事件发生了,问一种可能导致其发生的事件的概率。
P(Bi)是在试验前就知道的(如Bi病的发病率)称为先验概率。
P(Bi∣A)为观察到事件A发生的条件下Bi的概率,称为后验概率
常用,B∪Bˉ=Ω情况下
P(B∣A)=P(B)P(A∣B)+P(Bˉ)P(A∣Bˉ)P(B)P(A∣B)

后验概率的大小很受先验概率选取的影响。


1.5 事件的独立性
两个事件的独立性
A 和 B 相互独立
简单定义
P(A∣B)=P(A)且P(B∣A)=P(B)P(A),P(B)>0
或
P(AB)=P(A)P(B)
A与B相互独立
零事件与任何事件都独立
互不相容:事件纵向互不发生
相互独立事件,一定相容
互不相容事件,一定不独立
相容事件,不一定独立
https://zhuanlan.zhihu.com/p/36607363
三个事件独立
⎩⎨⎧P(AB)=P(A)P(B)P(BC)=P(B)P(C)P(AC)=P(A)P(C)P(ABC)=P(A)P(B)P(C)
由此推出n个事件独立性的定义
推论

若把n个相互的卢的事件分为互不重叠的k组(k≤n),则每组中的事件进行事件运算后所得的k个事件相互独立。
例如
若A1,...,An相互独立A1ˉ,...Aˉn相互独立,A1∪A2,A3−A4,Aˉ5,A7,...,An相互独立
再由德摩根律
P(∪i=1nAi)=1−P(∩i=1nAˉi)=1−i=1∏nP(Aˉi)=i=1∏n(1−P(Ai))

伯努利概型(试验)
pic21
示例,每个同学去图书馆只有两种结果:结借书和不借书,借书的概率为p,每个同学是否借书相互独立,那么观察n个同学到图书馆的借书情况就构成一个n重伯努利的试验。
设w=(w1,w2,⋯,wn)为N重伯努利试验的一个样本点,如果其中有k个A,n-k个Aˉ,则有试验独立性知
P((w1,w2⋅,wn))=pkqn−k
记BK = “在n重伯努利试验中事件A恰好发生k次”(13)
所有属于Bk的基本事件的概率均为pkqn−k,又因为 Bk共有(kn)个样本点,由概率的有限可加性,
P(Bk)=(kn)pkqn−k
二项分布,直接由二项式定理得
k=0∑n(kn)pkqn−k=(p+q)n=∣p+(1−q)∣n=1
2.随机变量及其概率分布
很多随机试验的结果都与数值发生自然的联系,
名词定义一览
一般地,设A为随机事件,则一定可以通过下述方法使他与数值发生联系
IA(w)={1,w∈A0,w∈/A
称IA为A的示性函数。
随机变量random variable
(Ω,F,P)是一个概率基本功华北,X是定义在Ω上的实质函数,如果对任意实数x,{X≤x}是随机事件,即{w:X(w)≤x}∈F,则称X为随机变量。
设X为随机变量,由事件域的性质,有一下极限表达

分布律
有些随机变量,它全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量,例如S1例1中的随机变量 X,它只可能取 0,1,2,3四个值,它是一个离散型随机变量。又如某城市的 120 急救电话台一昼夜收到的呼唤次数也是离散型随机变量。若以 T 记某元的寿命,它所可能取的值充满一个区间,是无法按一定次序一一列举出来的,因而它是一个非离散型的随机变量.本节只讨论离散型随机变量
设离散型随机变量 的概率,即事件⟨X−xk⟩P⟨X=xk⟩X 所有可能取的值为 xk(k=1,2,⋯),X 取各个可能值的概率,为=pk,k=1,2,⋯.(2.1)
称该式为离散性随机变量X的分布律,分布律也可用表格表示
| X |
x1 |
x2 |
| pk |
p1 |
p2 |
分布函数(简称分布)
设X是(Ω,F,P)上的随机变量,称实变实值函数
F(x)=P(X≤x),−∞<x<∞
为X的分布函数,如果X的分布函数为F(x),则称X服从分布F(x),记为X~F(x)
对于任意实数x1,x2(x1<x2),有
P{x1<X⩽x2}=P{X⩽x2}−P⟨X⩽x1⟩=F(x2)−F(x1),(3.1) 因此,若已知 X 的分布函数,我们就知道 X 落在任一区间(x1,x2]上的概率,从
这个意义上说,分布函数完整地描述了随机变量的统计规律性.
推论
对任意x,有$0\le F(x)\le 1 $,此外对任意实数a<b
有
P(a<X≤b)=P(X≤b)−P(X≤a)=F(b)−F(a)
类似可证 Ω={X<∞}
P(X>x)=P(X<∞)−P(X≤x)=1−F(x)
基本性质
设随机变量X的分布函数为F(x),则
- F(x)是x的单调增函数
- F(x)是x的右连续函数 F(x+0) = F(x)
渐进性 $F(\infty) := lim_{x\to \infty} F(x) = 1, $$F(-\infty) := lim_{x\to -\infty} F(x) = 0, $
即使随机变量X和Y的分布函数相同,称X与Y同分布,不能认为X=Y
跳跃值
如
F(x)=⎩⎨⎧0,41,43,1,x<−1,−1⩽x<2,2⩽x<3,x⩾3.
跳跃值分别为1/4,1/2,1/4
离散性随机变量
0-1分布
退化分布(单点分布),X是Ω上恒为常值的随机变量,即存在常数a使得对任何w∈Ω,有X(w)=a,则X的分布函数为
F(x)={0,x<a1,x≥a
分布律
P{X=k}=pk(1−p)1−k,k=0,1(0<p<1)
两点分布(伯努利分布)

二项分布
P{X=k}=(kn)pkqn−k,k=0,1,2,⋯,n.
并记为 X~b(n,p)
当n=1时,二项分布即为伯努利分布,
注意
(kn)=(n−kn)b(k;n,p)=b(n−k;n,1−p)


泊松分布
设随机变量 X 所有可能取的值为 0,1,2,⋅⋅⋅,而取各个值的概率为P⟨X=k⟩=k!λke−λ,k=0,1,2,⋅⋅⋅,其中 λ>0 是常数. 则称 X 服从参数为λ 的泊松分布,记为X∼π(λ).
这段可以省掉
limn→∞(kn)pnk(1−pn)n−k=k!λke−λ

当p很小 <= 0.05 n较大 >= 20
使用近似公式。
(kn)pk(1−p)n−k≈k!λke−λ(其中λ=np).
也就是说以 n,p为参数的二项分布的概率值可以由参数为λ=np 的泊松分布的概率值近似.上式也能用来作二项分布概率的近似计算.

一道纯离散性

连续性随机变量
概率密度
一般,如上节例 2 中的随机变量那样,如果对于随机变量 X 的分布函数F(x),存在非负可积函数 f(x) ,使对于任意实数 x 有
F(x)=∫−∞xf(t)dt,
则称 X 为连续型随机变量,f(x)称为 X 的概率密度函数,简称概率密度.

均匀分布
若连续型随机变量 X 具有概率密度
f(x)=⎩⎨⎧b−a1,0,a<x<b,其他,
则称 X 在区间(a,b)上服从均匀分布,记为X∼U(a,b).
易知f(x)⩾0,且∫−∞∞f(x)dx=1.
分布函数
F(x)=⎩⎨⎧0,x≤ab−ax−a,a<x<b1,x≥b

指数分布
若连续型随机变量X 的概率密度为
f(x)=⎩⎨⎧θ1e−x/θ,0,x>0,其他,
其中 θ>0 为常数,则称 X 服从参数为θ 的指数分布 .
X∼E(λ)
分布函数
F(x)={1−e−θx,x≥00,x<0
无记忆性,例如解释某元件的工作寿命,在已知元件已工作sh的条件下,再工作th以上的概率与已工作的事件s无关。
P(X>s+t∣X>s)=e−λt=P(X>t)
正态分布
概率密度
f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<∞
σ读作 \sigma
其中μ,σ(σ>0)为常数,则称 X 服从参数为μ,σ 的正态分布或高斯(Gauss)分布,记为X∼N(μ,σ2).
分布函数
F(x)=2πσ1∫−∞xe−2σ2(y−μ)2dy,−∞<x<∞
性质

标准正态函数
给定不同的μ,σ只需N(0,1)的分布表就行
而标准正态函数的概率密度、分布函数分别记作φ(x),Φ(x)
φ(x)=2π1e2−x2,Φ(x)=2π1∫−∞xe2−t2dt.Φ(−x)=1−Φ(x)
转化?
P(a<X≤b)=Φ(σb−μ)−Φ(σa−μ)
若X∼N(μ,σ2),则Y=σX−μ∼N(0,1)
正态随机变量的线性函数仍为正态随机变量。
标准正态函数分布函数制表请见最后
例题


随机变量函数及其分布
离散性随机变量函数的分布,他的分布律可直接从X的分布律求得

连续型随机变量


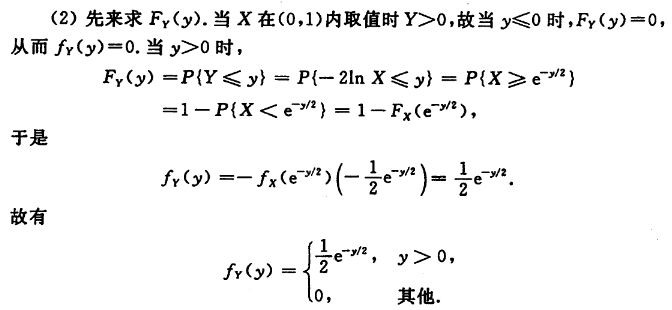
积分转化法



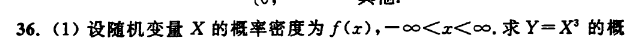

reference
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-10;
const double pi = acos(-1);
double f(double x)
{
return exp(-pow(x, 2) / 2) / sqrt(2 * pi);
}
double simpson(double l, double r)
{
return (r - l) * (f(l) + f(r) + 4 * f((l + r) / 2)) / 6;
}
double solve(double l, double r, double ans)
{
double m = (l + r) / 2, a = simpson(l, m), b = simpson(m, r);
if (fabs(a + b - ans) < eps)
return ans;
return solve(l, m, a) + solve(m, r, b);
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
cout.setf(ios::fixed);
double L = -7, R = 0;
freopen("out_with_estimator", "w", stdout);
cout << " x ";
cout << left << setprecision(2);
for (double col = 0.0; col <= 0.09; col += 0.01) {
cout << setw(6) << col << ' ';
}
cout << endl;
for (double row = 0.0; fabs(row - 4.0) > eps; row += 0.1) {
cout << setw(3) << setprecision(1);
cout << row << " ";
cout << setw(6) << setprecision(4);
for (double col = row; fabs(col - row - 0.1) > eps; col += 0.01) {
cout << solve(L, col, simpson(L, col)) << ' ';
}
cout << endl;
}
return 0;
}

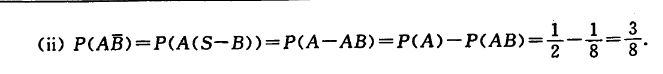
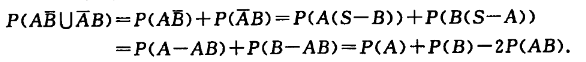




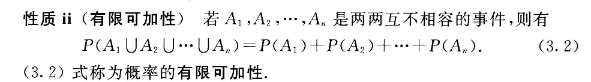



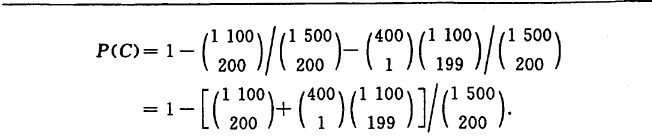























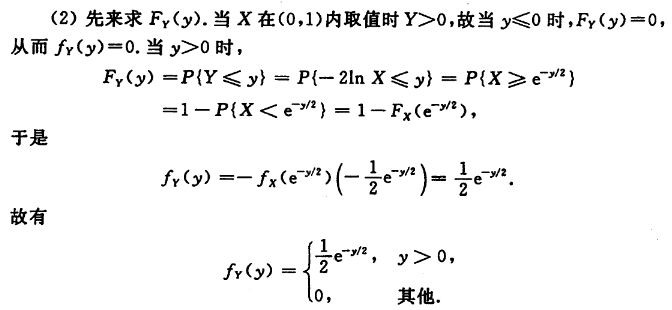



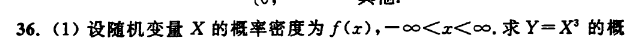

test
回复删除连续型随机变量没有分布律。
回复删除